SWTOR – Les méthodes mathématiques d’équilibrage

Application aux différentes classes par Hugo, à l'origine du projet LogAnalyzer.

L’équilibrage est un sujet complexe. Plusieurs méthodes sont employées pour viser l’équilibre, aucune n’est parfaite, mais la méthode mathématique a l’avantage d’être plus précise, malgré certains éléments d’incertitude. Je vais tenter d’expliquer cette méthode dans le cas de l’équilibrage des classes, en voyant d’une part la théorie (on va essayer d’éviter les formules mathématiques à rallonge !) et d’autre un exemple pratique.

Théorie

Qu’est-ce que l’équilibrage ?

Le principe de l’équilibre est d’obtenir une égalité entre deux membres. En appliquant une même fonction mathématique à deux classes différentes, il faut tendre à une égalité, ou à défaut à un écart faible.

Nous allons appeler ƒ notre fonction, qui prendra en paramètre notre classe c. L’objectif à atteindre est donc ƒ(c1) ≈ ƒ(c2) où c1 et c2 sont nos deux classes à comparer. L’approximation (signe ≈) signifie que l’on va viser  un écart faible. C’est à dire qu’on souhaite avoir un rapport ƒ(c1)/ƒ(c2) le plus proche possible de 1 (idéalement inférieur à 1%).

J’espère que jusqu’ici je ne vous ai pas perdu ! C’était le principal de la théorie de l’équilibrage. Le travail à effectuer désormais est de définir la fonction ƒ.

Et on équilibre quoi ?

Pour ce faire, il est nécessaire de déterminer les différentes variables à prendre en compte au sein d’une classe. Tout d’abord, le niveau et l’équipement ne rentrent pas en compte. On ne souhaite pas équilibrer d’un personnage à l’autre, mais bel et bien deux classes différentes.

Les éléments qui caractérisent une classe sont (pour simplifier) les capacités/sorts de cette classe, qui s’appliquent dans un cas précis (nous n’aurons pas les mêmes skills en JcE qu’en JcJ par exemple). Je vais passer outre les fonctionnements plus complexes comme la différence des ressources afin de simplifier l’explication, mais il est bien entendu que ces éléments sont à prendre en compte.

La fonction va donc prendre en compte les différentes capacités s’appliquant (JcE vs JcJ), ce qui va nous donner une forme de somme (symbole ). Celle-ci prend donc la forme suivante :

On effectue une somme sur l’ensemble des skills (de i=0 à n, n étant le nombre de skills) d’une seconde fonction g qui calcule le “poids” de la capacité s.

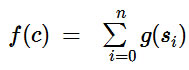
Passons à la définition de g désormais ! C’est là que toute la magique s’opère ! Encore une fois, nous devons déterminer les composantes variables d’une capacité/skill. Encore une fois dans un but de simplification, nous allons uniquement prendre en compte certains éléments, ceux-ci sont :

• Le coût en ressource (en pratique, celui-ci devrait être relativisé par rapport au type de ressource de la classe, mais nous avons occulté ce point)
• Le type d’effet (dégâts, soins, menace) qui va être un facteur à appliquer sur
• La quantité d’effet (points de vie soignés, dégâts effectués, …)

Il y a bien d’autres éléments à prendre en compte, tels que les effets supplémentaires (ralentissement, stun, déplacement, …). Cependant vous pouvez déjà noter qu’autant certains éléments sont facilement quantifiables (coût en ressource, quantité), autant d’autres sont plus subjectifs (type d’effet) et ne peuvent être déterminés numériquement : il faut estimer. C’est là que la partie complexe de l’équilibrage mathématique entre en compte : c’est au fur et à mesure d’essais et de modifications que nous tendrons vers des valeurs optimales, mais il est difficile de connaître précisément ces valeurs. (Je ne dis pas impossible, car mathématiquement, nous pourrions y arriver, mais cela requiert un autre type de calculs et je ne souhaite pas vous embrouiller encore plus avec ça !)

Notre fonction g va donc prendre en paramètres les éléments sus-nommés :

Où Q représente la quantité d’effet, E le type de l’effet et R le coût. Cette fonction signifie que nous prenons les apports de la capacité s et que nous les divisons par leur coût. L’apport est représenté sous la forme Q*E, ce qui signifie que la valeur est conditionnée par le type d’effet. 200 points de dégâts appliqués n’auront pas le même apport que 200 points de vie soignés.

Encore une fois, cette fonction est simplifiée et ne prend pas en compte l’ensemble des paramètres possibles. Il n’est par exemple pas pris en compte qu’effectuer des dégâts sur une cible génère aussi de la menace. (Auquel cas, il faudrait additioner les apports des différents types dans le cas d’un personnage tank ; ou ajouter la menace comme coût dans le cas d’un DPS. Je vous avais dit, c’est compliqué !)

Nous avons vu la théorie, passons à un exemple pratique. 

Pratique

Premier calcul

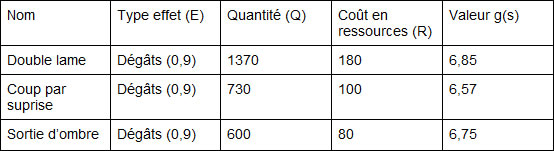
J’ai d’un côté un consulaire érudit DPS ; d’un autre un consulaire ombre DPS. Je veux les comparer sur le plan JcJ. Je vais déterminer 3 skills pour chacune des classes qui seront complètement inventés au niveau de leurs valeurs, et tenter de détailler le processus d’équilibrage. Voyons les skills de l’érudit :

Et ceux de l’ombre :

J’ai pour chaque skill/capacité calculé la valeur de g(s) via la formule citée plus haut.

Pour l’érudit, la fonction ƒ(c)retourne 13,86 ; pour l’ombre, 20,17. On note d’ores et déjà un écart important, mais nous allons calculer celui-ci tout de même. En effectuant le calcul 13,8620,17 nous obtenons la valeur 0,687159147 soit un écart de plus de 31% entre les deux classes. Ceci n’est pas satisfaisant.

Ajustement

Il s’agit alors de redéfinir les valeurs ou bien à la hausse pour le consulaire, ou bien à la baisse pour l’ombre. (Le choix va être déterminé par rapport aux valeurs renvoyées par les calculs sur autres classes.) Admettons que nous baissons l’ombre, nous déterminons ces nouvelles valeurs :

La somme des différentes valeurs nous donne 13,74. Ceci est déjà plus proche du score de l’érudit. Calculons maintenant la différence :  nous donne 1,00873 soit +0,87% pour le consulaire. Nous avons atteint notre objectif, à savoir avoir moins d’un pourcent de différence entre les deux classes.

La méthode expliquée ci-dessus est une méthode théorique. Elle prend en compte les valeurs mises en jeu, et doit être affinée pour correspondre avec les valeurs réelles. Ceci peut se faire par le biais de calculs concernant les données extraites des enregistrements effectués dans le jeu (ce sont notamment ces données qui remontent des alertes aux développeurs quant à l’équilibrage des différentes classes). Cependant cette modélisation mathématique permet de faire des estimations quant aux changements que l’on souhaite apporter aux valeurs.

Encore une fois, ce n’est ici qu’une méthode simplifiée afin de permettre à chacun de comprendre le fonctionnement et le raisonnement. Les véritables outils mis en oeuvre comprennent des fonctions bien plus complexes, et beaucoup plus de variables. De plus, j’insiste sur le fait que ce n’est pas parce que la méthode est mathématiques qu’elle est parfaite. On a pu le voir, certaines variables demandent des estimations, et des affinages qui auront lieu avec du temps et des données supplémentaires. C’est pourquoi toute optimisée qu’elle soit n’importe quelle fonction ne saurait être précise à 100%.

Hugo